I will be speaking at the Models of Peano Arithmetic seminar on Wednesday, September 21, 2016 on “Ramsey Quantifiers”. The abstract is listed on the NYLogic site, but for context I wanted to provide some thoughts on why I am digging up this older topic.
This theory piqued my interest while I was studying the lattice problem for models of PA. In studying this problem, it became apparent that certain combinatorial properties of representations of lattices were important. Let me preface this by saying that much of this information is in The Structure of Models of Peano Arithmetic, by Kossak and Schmerl, in Chapter 4 on Substructure Lattices.
A representation of a lattice 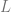 on a set
on a set 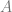 is an injection
is an injection  (where Eq(A) is the set of equivalence relations on the set A), such that for each
(where Eq(A) is the set of equivalence relations on the set A), such that for each  ,
,  is the trivial relation and
is the trivial relation and  is the discrete relation . Given
is the discrete relation . Given  and a set
and a set  , the function
, the function 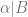 is defined by
is defined by  for each
for each 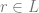 . Two representations of the same lattice,
. Two representations of the same lattice,  are called isomorphic if there is a bijection
are called isomorphic if there is a bijection  respecting the equivalence relations; that is, for each
respecting the equivalence relations; that is, for each 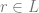 and
and 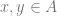 ,
, 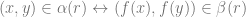 .
.
The Lattice 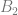
The lattice  is the Boolean Algebra on a 2 element set: (with
is the Boolean Algebra on a 2 element set: (with 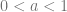 and
and 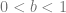 ). Gaifman proved that every model
). Gaifman proved that every model 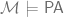 has an elementary end extension
has an elementary end extension  such that the interstructure lattice
such that the interstructure lattice 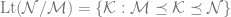 is isomorphic to
is isomorphic to 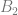 (in fact, Gaifman’s proof works for every finite Boolean algebra). But we can also form such an elementary extension by studying the appropriate representation of the lattice
(in fact, Gaifman’s proof works for every finite Boolean algebra). But we can also form such an elementary extension by studying the appropriate representation of the lattice 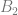 .
.
Given a model 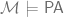 , there is a particularly simple representation on the set of pairs of elements of
, there is a particularly simple representation on the set of pairs of elements of 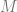 , denoted
, denoted ![[M]^2](https://s0.wp.com/latex.php?latex=%5BM%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) . This representation is defined by letting
. This representation is defined by letting 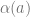 be the equivalence relation determined by equality on the first coordinate, and
be the equivalence relation determined by equality on the first coordinate, and 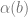 be the equivalence relation determined by equality on the second coordinate. This representation is definable in
be the equivalence relation determined by equality on the second coordinate. This representation is definable in 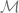 , by using the normal coding of pairs of numbers (Cantor’s pairing function) and the induced projection functions.
, by using the normal coding of pairs of numbers (Cantor’s pairing function) and the induced projection functions.
The key lemma we need to construct the elementary extension is that for any definable equivalence relation  on
on ![[\mathcal{M}]^2](https://s0.wp.com/latex.php?latex=%5B%5Cmathcal%7BM%7D%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) , there is a definable subset
, there is a definable subset 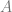 of
of ![[\mathcal{M}]^2](https://s0.wp.com/latex.php?latex=%5B%5Cmathcal%7BM%7D%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) such that
such that 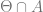 is either discrete, trivial,
is either discrete, trivial, 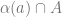 or
or 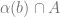 , and
, and 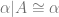 . The underlying combinatorics here is a generalization of Ramsey’s theorem for pairs, first proved by Erdős and Rado: given any equivalence relation
. The underlying combinatorics here is a generalization of Ramsey’s theorem for pairs, first proved by Erdős and Rado: given any equivalence relation  on
on ![[\mathcal{M}]^2](https://s0.wp.com/latex.php?latex=%5B%5Cmathcal%7BM%7D%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) , there is an infinite set
, there is an infinite set  such that
such that ![\Theta \cap [X]^2](https://s0.wp.com/latex.php?latex=%5CTheta+%5Ccap+%5BX%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) is either discrete, trivial,
is either discrete, trivial, ![\alpha(a) \cap [X]^2](https://s0.wp.com/latex.php?latex=%5Calpha%28a%29+%5Ccap+%5BX%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) or
or ![\alpha(b) \cap [X]^2](https://s0.wp.com/latex.php?latex=%5Calpha%28b%29+%5Ccap+%5BX%5D%5E2&bg=ffffff&fg=666666&s=0&c=20201002) . Note that this
. Note that this  is just an infinite set of numbers, not of pairs.
is just an infinite set of numbers, not of pairs.
This is similar to the key lemma needed when constructing minimal extensions. If  is a model, a minimal extension
is a model, a minimal extension  is an elementary extension such that there are no proper intermediate elementary structures (that is, if
is an elementary extension such that there are no proper intermediate elementary structures (that is, if 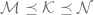 , then
, then 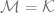 or
or  ). In that case, we consider any infinite definable set
). In that case, we consider any infinite definable set 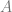 and show that for any definable equivalence relation
and show that for any definable equivalence relation  on
on 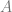 , there is an infinite definable
, there is an infinite definable  such that that
such that that  is either discrete or trivial. The main difference between these two cases is the first order expressibility of these statements. Stating that there is an infinite subset
is either discrete or trivial. The main difference between these two cases is the first order expressibility of these statements. Stating that there is an infinite subset  on which
on which  is discrete or trivial can be expressed in the language of first order arithmetic:
is discrete or trivial can be expressed in the language of first order arithmetic:
![[\exists x \in A \forall w \exists y \in A (y > w \wedge (x, y) \in \Theta)] \vee [\forall w \exists y > w (y \in A \wedge \forall x < y (x \in A \rightarrow (x, y) \not \in \Theta))]](https://s0.wp.com/latex.php?latex=%5B%5Cexists+x+%5Cin+A+%5Cforall+w+%5Cexists+y+%5Cin+A+%28y+%3E+w+%5Cwedge+%28x%2C+y%29+%5Cin+%5CTheta%29%5D+%5Cvee+%5B%5Cforall+w+%5Cexists+y+%3E+w+%28y+%5Cin+A+%5Cwedge+%5Cforall+x+%3C+y+%28x+%5Cin+A+%5Crightarrow+%28x%2C+y%29+%5Cnot+%5Cin+%5CTheta%29%29%5D&bg=ffffff&fg=666666&s=0&c=20201002) .
.
Even though it appears, at first, we want to say “There is an infinite set” where something holds (which would appear to be a second-order quantifier), we can state this in first order (because by “infinite” we really mean “unbounded”).
In the Erdős-Rado result, something appears to be significantly different, however. We must state: “there is an infinite set 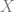 such that either (i) for all
such that either (i) for all 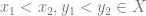 ,
, 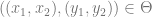 , (ii) for all
, (ii) for all 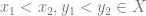 ,
, 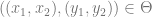 if and only if
if and only if  , (iii) for all
, (iii) for all 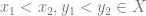 ,
, 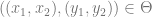 if and only if
if and only if 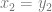 , or (iv) for all
, or (iv) for all 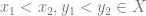 ,
, 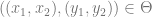 if and only if
if and only if 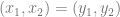 . In this case, we cannot replace the second-order quantifier with first order ones asserting unboundedness of some property, because we wish to quantify over pairs of elements from that (unbounded) set.
. In this case, we cannot replace the second-order quantifier with first order ones asserting unboundedness of some property, because we wish to quantify over pairs of elements from that (unbounded) set.
After thinking about this for awhile, my advisor mentioned a section in Chapter 10 of The Structure of Models of Peano Arithmetic, which discusses an extra quantifier called a “Ramsey quantifier”, denoted 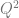 . This quantifier extends the language of first order logic by binding two variables. The intended interpretation of
. This quantifier extends the language of first order logic by binding two variables. The intended interpretation of 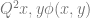 is “There is an infinite set
is “There is an infinite set 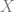 such that for all
such that for all  ,
,  holds.” This is exactly the kind of extension to the language that I needed, and I hope to talk about some of the basic results in the theory of Peano Arithmetic in this augmented language (with induction for all formulas in the extended language).
holds.” This is exactly the kind of extension to the language that I needed, and I hope to talk about some of the basic results in the theory of Peano Arithmetic in this augmented language (with induction for all formulas in the extended language).
has an undefinable, inductive subset
such that the expansion
is pointwise definable. Enayat later showed that there are many models with the property that every expansion upon adding a predicate for an undefinable class is pointwise definable. We refer to models with this property as Enayat models. That is, a model
is Enayat if for each undefinable class
, the expansion
is pointwise definable. In this talk we show that a model is Enayat if it is countable, has no proper cofinal submodels and is a conservative extension of each of its elementary cuts.
